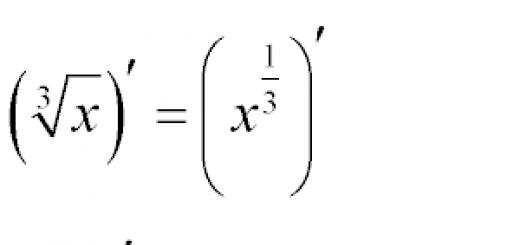До появления калькуляторов студенты и преподаватели вычисляли квадратные корни вручную. Существует несколько способов вычисления квадратного корня числа вручную. Некоторые из них предлагают только приблизительное решение, другие дают точный ответ.

Шаги

Разложение на простые множители

Разложите подкоренное число на множители, которые являются квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа – числа, из которых можно извлечь целый квадратный корень. Множители – числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как √25 = 5, √36 = 6, √49 = 7. Квадратные множители – это множители, которые являются квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.

• Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 – это квадратное число. Разделив 400 на 25, вы получите 16. Число 16 также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
• Записать это можно следующим образом: √400 = √(25 х 16).

1. Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть √(а х b) = √a x √b. Воспользуйтесь этим правилом и извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.

   • В нашем примере извлеките корень из 25 и из 16.
     • √(25 х 16)
     • √25 х √16
     • 5 х 4 = 20

2. Если подкоренное число не раскладывается на два квадратных множителя (а так происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.

   • Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
     • = √(49 х 3)
     • = √49 х √3
     • = 7√3

3. Если нужно, оцените значение корня. Теперь можно оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.

   • Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
     • Этот метод также работает с большими числами. Например, рассмотрим √35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (√25 = 5) и 36 (√36 = 6). Таким образом, значение √35 расположено между 5 и 6. Так как значение √35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что √35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 - мы были правы.

4. Еще один способ – разложите подкоренное число на простые множители . Простые множители – числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.

   • Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, √45 = √(3 х 3 х 5). 3 можно вынести за знак корня: √45 = 3√5. Теперь можно оценить √5.
   • Рассмотрим другой пример: √88.
     • = √(2 х 44)
     • = √ (2 х 4 х 11)
     • = √ (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
     • = 2√(2 х 11) = 2√2 х √11. Теперь можно оценить √2 и √11 и найти приблизительный ответ.

   Вычисление квадратного корня вручную

   При помощи деления в столбик

   1. Этот метод включает процесс, аналогичный делению в столбик, и дает точный ответ. Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как "7 95 20 78 91 82, 47 89 70".

      • Для примера вычислим квадратный корень числа 780,14. Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде "7 80, 14". Это нормально, что первая слева цифра является непарной цифрой. Ответ (корень из данного числа) будете записывать справа сверху.

   2. Для первой слева пары чисел (или одного числа) найдите наибольшее целое число n, квадрат которого меньше или равен рассматриваемой паре чисел (или одного числа). Другими словами, найдите квадратное число, которое расположено ближе всего к первой слева паре чисел (или одному числу), но меньше ее, и извлеките квадратный корень из этого квадратного числа; вы получите число n. Напишите найденное n сверху справа, а квадрат n запишите снизу справа.

      • В нашем случае, первым слева числом будет число 7. Далее, 4 < 7, то есть 2 2 < 7 и n = 2. Напишите 2 сверху справа - это первая цифра в искомом квадратном корне. Напишите 2×2=4 справа снизу; вам понадобится это число для последующих вычислений.

   3. Вычтите квадрат числа n, которое вы только что нашли, из первой слева пары чисел (или одного числа). Результат вычисления запишите под вычитаемым (квадратом числа n).

      • В нашем примере вычтите 4 из 7 и получите 3.

   4. Снесите вторую пару чисел и запишите ее около значения, полученного в предыдущем шаге. Затем удвойте число сверху справа и запишите полученный результат снизу справа с добавлением "_×_=".

      • В нашем примере второй парой чисел является "80". Запишите "80" после 3. Затем, удвоенное число сверху справа дает 4. Запишите "4_×_=" снизу справа.

   5. Заполните прочерки справа.

      • В нашем случае, если вместо прочерков поставить число 8, то 48 х 8 = 384, что больше 380. Поэтому 8 - слишком большое число, а вот 7 подойдет. Напишите 7 вместо прочерков и получите: 47 х 7 = 329. Запишите 7 сверху справа - это вторая цифра в искомом квадратном корне числа 780,14.

   6. Вычтите полученное число из текущего числа слева. Запишите результат из предыдущего шага под текущим числом слева, найдите разницу и запишите ее под вычитаемым.

      • В нашем примере, вычтите 329 из 380, что равно 51.

   7. Повторите шаг 4. Если сносимой парой чисел является дробная часть исходного числа, то поставьте разделитель (запятую) целой и дробной частей в искомом квадратном корне сверху справа. Слева снесите вниз следующую пару чисел. Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением "_×_=".

      • В нашем примере следующей сносимой парой чисел будет дробная часть числа 780.14, поэтому поставьте разделитель целой и дробной частей в искомом квадратном корне сверху справа. Снесите 14 и запишите снизу слева. Удвоенным числом сверху справа (27) будет 54, поэтому напишите "54_×_=" снизу справа.

   8. Повторите шаги 5 и 6. Найдите такое наибольшее число на место прочерков справа (вместо прочерков нужно подставить одно и тоже число), чтобы результат умножения был меньше или равен текущему числу слева.

      • В нашем примере 549 х 9 = 4941, что меньше текущего числа слева (5114). Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 - 4941 = 173.

   9. Если для квадратного корня вам необходимо найти больше знаков после запятой, напишите пару нулей у текущего числа слева и повторяйте шаги 4, 5 и 6. Повторяйте шаги, до тех пор пока не получите нужную вам точность ответа (число знаков после запятой).

   Понимание процесса

   Для усвоения данного метода представьте число, квадратный корень которого необходимо найти, как площадь квадрата S. В этом случае вы будете искать длину стороны L такого квадрата. Вычисляем такое значение L, при котором L² = S.

   Задайте букву для каждой цифры в ответе. Обозначим через A первую цифру в значении L (искомый квадратный корень). B будет второй цифрой, C - третьей и так далее.

   Задайте букву для каждой пары первых цифр. Обозначим через S a первую пару цифр в значении S, через S b - вторую пару цифр и так далее.

   Уясните связь данного метода с делением в столбик. Как и в операции деления, где каждый раз нас интересует только одна следующая цифра делимого числа, при вычислении квадратного корня мы последовательно работаем с парой цифр (для получения одной следующей цифры в значении квадратного корня).

   1. Рассмотрим первую пару цифр Sa числа S (Sa = 7 в нашем примере) и найдем ее квадратный корень. В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен S a (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa < (A+1)²). В нашем примере, S1 = 7, и 2² ≤ 7 < 3²; таким образом A = 2.

      • Допустим, что нужно разделить 88962 на 7; здесь первый шаг будет аналогичным: рассматриваем первую цифру делимого числа 88962 (8) и подбираем такое наибольшее число, которое при умножении на 7 дает значение меньшее или равное 8. То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8 < 7×(d+1). В этом случае d будет равно 1.

Слайд 2

Цели урока:

Повторить определение арифметического квадратного корня. Ввести и доказать теорему о квадратном корне из произведения. Научиться находить . Проверить знания и умения с помощью самостоятельной работы.

Слайд 3

Квадратный корень из произведения

План урока: Актуализация знаний. Изучение нового материала. Закрепление формулы на примерах. Самостоятельная работа. Подведение итогов. Задание на дом.

Слайд 4

Здравствуйте, ребята!

Повторим: 2. Что называется арифметическим квадратным корнем из числа 3. При каком значении выражение имеет смысл? 1. Как называется выражение

Слайд 5

Найдите:

1) 2) 3) 7 или или 7

Слайд 6

Сегодня мы познакомимся с одним из свойств арифметического квадратного корня. Введем и докажем теорему о квадратном корне из произведения, рассмотрим примеры её применения. Затем Вам будут предложены задания для самопроверки. Желаю удачи!

Слайд 7

Попробуем решить

Рассмотрим арифметический корень Найдите значение выражения: Значит, Итак, корень из произведения двух чисел равен произведению корней из этих чисел.

Слайд 8

Корень из произведения неотрицательных множителей равен произведению корней из этих множителей. Если то Теорема

Слайд 9

Квадратный корень из произведения

Доказательство: значит, - имеют смысл. 4. Вывод: (т.к. произведение двух неотрицательных чисел неотрицательно)‏ 5. Итак,

Слайд 10

Мы рассмотрели доказательство теоремы об извлечении квадратного корня из произведения. Перейдём к практической работе. Сейчас я вам покажу как применяется эта формула при решении примеров. Решайте вместе со мной.

Слайд 11

Вычислите значение квадратного корня, используя теорему о корне из произведения: Решаем примеры:

Слайд 12

Решаем примеры:

2. Найдите значение выражения:

Слайд 13

Быстрый счёт

А я догадался, как можно использовать эту формулу для быстрых вычислений. Смотри и учись.

Слайд 14

Вариант 1 Вариант 2 Предлагаю вам примеры для самостоятельного решения.

Формулы корней. Свойства квадратных корней.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно "не очень..."
И для тех, кто "очень даже...")

В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.

Формулы корней, свойства корней и правила действий с корнями - это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да...

Начнём с самой простой. Вот она:

Если Вам нравится этот сайт...

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся - с интересом!)

можно познакомиться с функциями и производными.

СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ,

СТЕПЕННАЯ ФУНКЦИЯ IV

§ 79. Извлечение корней из произведения и частного

Теорема 1. Корень п -й степени из произведения положительных чисел равен произведению корней п -й степени из сомножителей, то есть при а > 0, b > 0 и натуральном п

n √ab = n √a n √b . (1)

Доказательство. Напомним, что корень п -й степени из положительного числа ab есть такое положительное число, п -я степень которого равна ab . Поэтому доказать равенство (1) - это все равно, что доказать равенство

(n √a n √b ) n = ab .

По свойству степени произведения

(n √a n √b ) n = (n √a ) n (n √b ) n =.

Но по определению корня п -й степени (n √a ) n = а , (n √b ) n = b .

Поэтому (n √a n √b ) n = ab . Теорема доказана.

Требование а > 0, b > 0 существенно лишь для четного п , поскольку при отрицательных а и b и четном п корни n √a и n √b не определены. Если же п нечетно, то формула (1) справедлива для любых а и b (как положительных, так и отрицательных).

Примеры: √16 121 = √16 √121 = 4 11 = 44.

3 √-125 27 = 3 √-125 3 √27 = -5 3 = - 15

Формулу (1) полезно использовать при вычислении корней, когда подкоренное выражение представляется в виде произведения точных квадратом. Например,

√153 2 -72 2 = √ (153+ 72) (153-72) = √225 81 = 15 9 = 135.

Теорему 1 мы доказали для случая, когда под знаком радикала в левой части формулы (1) стоит произведение двух положительных чисел. На самом же деле эта теорема верна для любого числа положительных сомножителей, то есть при любом натуральном k > 2:

Следствие. Читая это тождество справа налево, мы получаем следующее правило умножения корней с одинаковыми.показателями;

Чтобы перемножить корни с одинаковыми показателями, достаточно перемножить подкоренные выражения, оставив показатель корня прежним.

Например, √3 √8 √6 = √3 8 6 = √144 = 12.

Теорема 2. Корень п -й степени из дроби, числитель и знаменатель которой - положительные числа, равен частному от деления корня той же степени из числителя на корень той же степени из знаменателя , то есть при а > 0 и b > 0

(2)

Доказать равенство (2)-это значит показать, что

По правилу возведения дроби в степень и определению корня n -й степени имеем:

Тем самым теорема доказана.

Требование а > 0 и b > 0 существенно лишь при четном п . Если же п нечетно, то формула (2) верна и для отрицательных значений а и b .

Следствие. Читая тождество справа налево, мы получаем следующее правило деления корней с одинаковыми показателями:

Чтобы разделить корни с одинаковыми показателями, достаточно разделить подкоренные выражения, оставив показатель корня прежним .

Например,

Упражнения

554. В каком месте доказательства теоремы 1 мы использовали то, что а и b положительны?

Почему при нечетном п формула (1) верна и для отрицательных чисел а и b ?

При каких значениях х верны данные равенства (№ 555-560):

555. √x 2 - 9 = √x -3 √х + 3 .

556. 4 √ (x - 2) (8 - x ) = 4 √х - 2 4 √ 8 - x

557. 3 √ (х + 1) (х - 5) = 3 √х +1 3 √х - 5 .

558. √ х (х + 1) (х + 2) = √ х √ (х + 1) √ (х + 2)

559. √ (х - а ) 3 = (√ х - а ) 3 .

560. 3 √ (х - 5) 2 = (3 √ х - 5 ) 2 .

561. Вычислить:

a) √ 173 2 - 52 2 ; в) √ 200 2 - 56 2 ;

б) √ 373 2 - 252 2 ; г) √ 242,5 2 - 46,5 2 .

562. В прямоугольном треугольнике гипотенуза равна 205 см, а один из катетов 84 см. Найти другой катет.

563. Во сколько раз:

555. х > 3. 556. 2 < х < 8. 557. х - любое число. 558. х > 0. 559. х > а . 560. х - любое число. 563. а) В три раза.